LCM and GCD of Two Numbers in Java

LCM of Two Numbers in Java

Let’s start discussing how to find LCM of two numbers in Java. We can find LCM in 2 ways: (1) by iterating over a loop (2) by using GCD

What is the Least Common Multiple (LCM)?

Its definition is self-explanatory. If there are two numbers x and y, LCM is a positive number and the smallest of all the common multiples of both x and y.

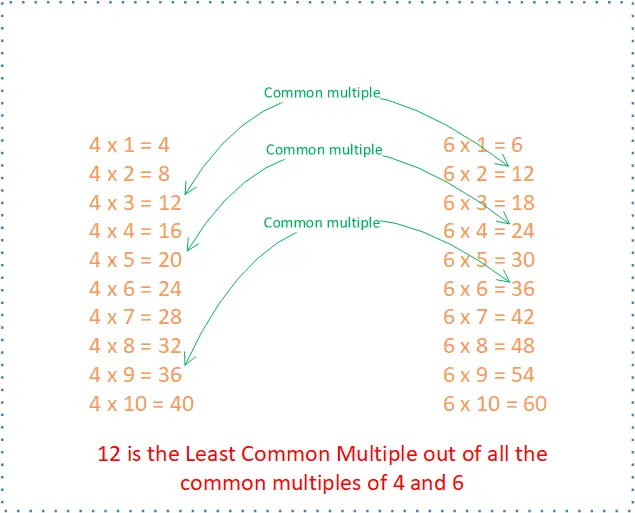
Finding LCM using Loops

1. Assume the biggest number of x and y is the LCM
2. To verify this assumption, divide the biggest number with x and y
3. If remainder is 0, then the biggest number is the LCM
4. If the remainder is not 0, then we need to go over the multiples of the biggest number and find for a number can be divided by both x and y evenly

package com.techstackjournal;

import java.util.Scanner;

public class LeastCommonMultiple {
	public static void main(String arg[]) {
		int num1, num2, mul, result;

		Scanner sc = new Scanner(System.in);
		System.out.println("Enter Number 1");
		num1 = sc.nextInt();
		System.out.println("Enter Number 2");
		num2 = sc.nextInt();
		sc.close();

		if (num1 > num2) {
			result = mul = num1;
		} else {
			result = mul = num2;
		}

		for (int i = 2; result % num1 != 0 || result % num2 != 0; i++) {
			result = mul * i;
		}
		
		System.out.printf("LCM of (%d,%d) is %d", num1, num2, result);
	}

}

Enter Number 1
3
Enter Number 2
4
LCM of (3,4) is 12

Finding LCM using GCD

Another method for finding LCM of 2 numbers (x and y) is dividing the product of x and y with GCD of x and y.

Formula: LCM(x,y) = (x*y) / gcd(x,y)

package com.techstackjournal;

import java.util.Scanner;

public class LCMExample2 {
	public static void main(String arg[]) {
		int num1, num2, mul, result;

		Scanner sc = new Scanner(System.in);
		System.out.println("Enter Number 1");
		num1 = sc.nextInt();
		System.out.println("Enter Number 2");
		num2 = sc.nextInt();
		sc.close();

		result = (num1 * num2) / findGCD(num1, num2);

		System.out.printf("LCM of (%d,%d) is %d", num1, num2, result);
	}

	public static int findGCD(int num1, int num2) {
		int rem;

		do {
			rem = num1 % num2;
			num1 = num2;
			num2 = rem;

		} while (rem != 0);

		return num1;
	}

}

Enter Number 1
18
Enter Number 2
30
LCM of (18,30) is 90

GCD of Two Numbers in Java

Let’s discuss how to find GCD of two numbers in Java. A GCD is a positive and largest integer among all the common divisors of two numbers. It is also called as Greatest Common Factor (GCF).

Greatest Divisor of 16 is 16 and the greatest divisor of 28 is 28. However, the Greatest Divisor of both 16 and 28 is 4. 2 also can divide both these numbers evenly, but after 2 only 4 can divide these 2 numbers, and no other number greater than 4 can divide these two numbers evenly. So, we call 4 as a Greatest Common Divisor.

The GCD of two numbers cannot be bigger than the smaller of the two numbers.

The GCD cannot be bigger than the smaller number of the 2 numbers, as it cannot divide the smaller number. For example, if given two numbers are 15 and 30 the GCD can’t be greater than 15.

Steps to find GCD

• Divide the greater number with the small number
• If smaller number exactly divides the greater number with a remainder of zero then smaller number is itself the GCD
• If smaller number couldn’t divide exactly, then consider the remainder as the divisor and the previous small number as the dividend
• Continue the same set of operations from start, until a 0 remainder is obtained
• When a 0 remainder is obtained the GCD will be in the dividend variable

Find GCD using Loop

package com.techstackjournal;

import java.util.Scanner;

public class GCDLoopExample {

	public static void main(String[] args) {
		int num1, num2, reminder;
		Scanner sc = new Scanner(System.in);

		System.out.println("Enter Number 1");
		num1 = sc.nextInt();
		System.out.println("Enter Number 2");
		num2 = sc.nextInt();
		sc.close();

		int dividend = num1;
		int divisor = num2;

		do {
			reminder = dividend % divisor;
			dividend = divisor;
			divisor = reminder;

		} while (reminder != 0);

		System.out.printf("GCD of (%d, %d) is %d", num1, num2, dividend);

	}

}

Enter Number 1
16
Enter Number 2
28
GCD of (16, 28) is 4

Find GCD using Recursion

package com.techstackjournal;

import java.util.Scanner;

public class GCDRecursionExample {

	public static void main(String[] args) {
		int num1, num2, gcdres;
		Scanner sc = new Scanner(System.in);

		System.out.println("Enter Number 1");
		num1 = sc.nextInt();
		System.out.println("Enter Number 2");
		num2 = sc.nextInt();
		sc.close();

		gcdres = gcd(num1, num2);

		System.out.printf("GCD of (%d, %d) is %d", num1, num2, gcdres);

	}

	static int gcd(int divisor, int dividend) {
		if (divisor == 0) {
			return dividend;
		} else {
			return gcd(dividend % divisor, divisor);
		}
	}

}

Enter Number 1
18
Enter Number 2
30
GCD of (18, 30) is 6

GCD simplifies finding LCM. Similarly, if you know LCM of two numbers you can calculate GCD of it.

Find GCD using LCM

package com.techstackjournal;

import java.util.Scanner;

public class GCDFromLCFExample {

	public static void main(String[] args) {
		int num1, num2, gcdres;
		Scanner sc = new Scanner(System.in);

		System.out.println("Enter Number 1");
		num1 = sc.nextInt();
		System.out.println("Enter Number 2");
		num2 = sc.nextInt();
		sc.close();

		gcdres = (num1 * num2) / lcf(num1, num2);

		System.out.printf("GCD of (%d, %d) is %d", num1, num2, gcdres);

	}

	static int lcf(int num1, int num2) {
		int result, mul;
		
		if (num1 > num2) {
			result = mul = num1;
		} else {
			result = mul = num2;
		}

		for (int i = 2; result % num1 != 0 || result % num2 != 0; i++) {
			result = mul * i;
		}

		return result;
	}

}

Enter Number 1
18
Enter Number 2
30
GCD of (18, 30) is 6